Application of Madqwick Quaternion Update and necessary data preparations

The aim of the project was to process the signals recorded by inertial measurement units. The LSM6DSL and LSM6DSV sensors used in the project are capable of measuring angular velocity with a 16-bit resolution. I processed the measured data in C#, after the measurement, integrating it into the system’s UI. However, numerous disturbing factors, such as noise and other forces acting on the sensor, influence the measurement results. To achieve more accurate data, it is essential to preprocess the data.

• Data Processing Method: The first solution applied was to filter out the harmonics of the incoming data. To do this, I decomposed the incoming signal into its harmonics using Fourier transformation.
• Distinguishing Noise from Actual Measurements: Through empirical methods, I determined the difference between the noise and the actual measurement, which allowed for the execution of extreme signal processing tasks.
• Inverse Fourier Transformation: To remove the unwanted harmonics, I used an inverse Fourier transformation, which enabled the attainment of clearer and more accurate measurement results.

The following four figures illustrate the results of the above processes, demonstrating the employed methods and their effectiveness in improving measurement accuracy.

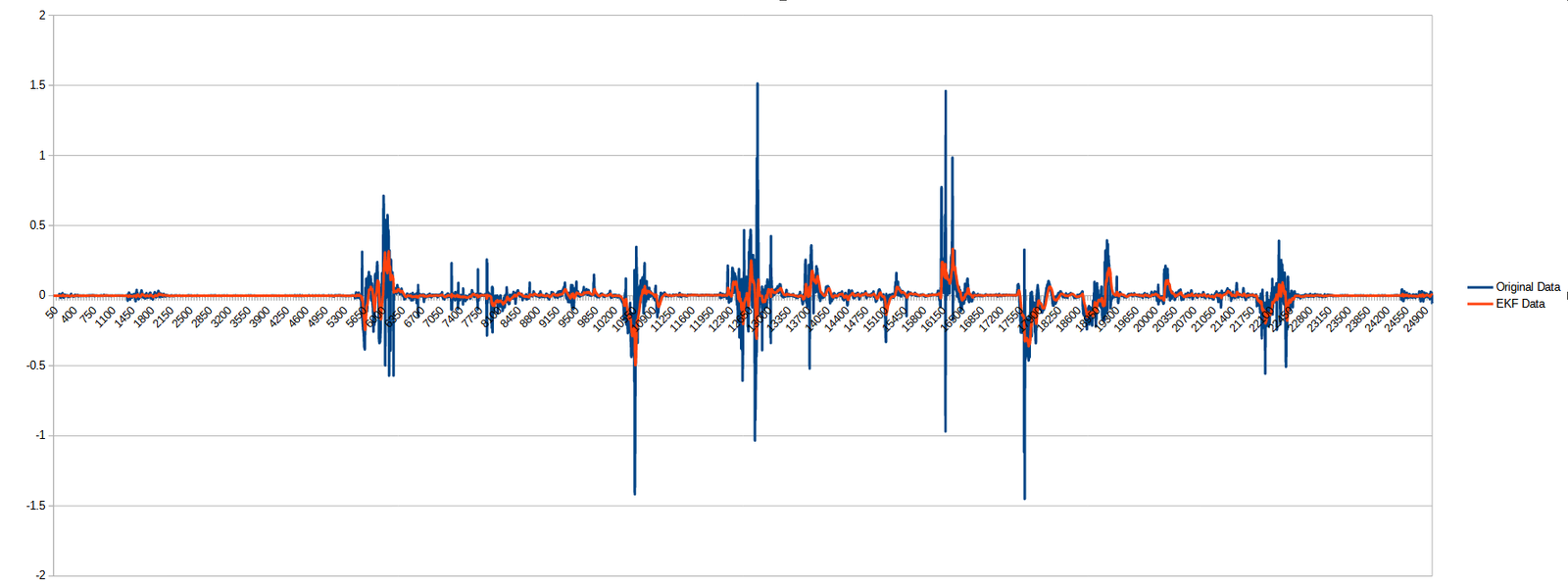
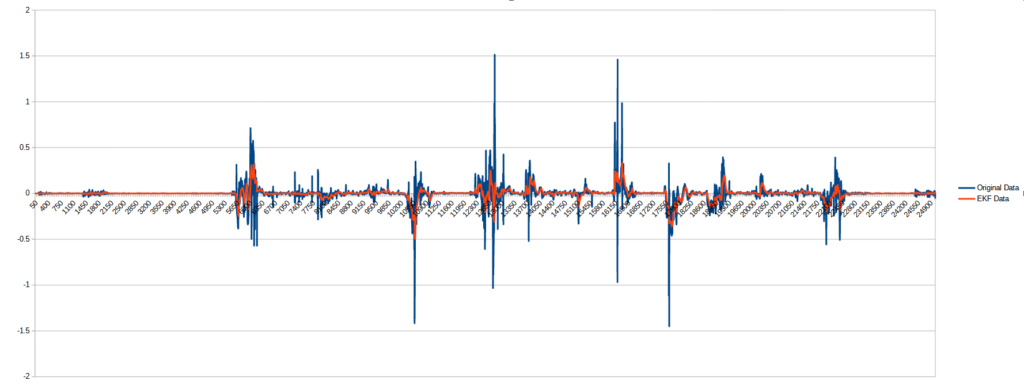
To eliminate the errors arising from the operation of the gyroscope, I applied the Extended Kalman Filter (EKF), which is a sophisticated algorithm used for state estimation in nonlinear systems. The EKF is an extension of the classical Kalman Filter, which is applicable to linear systems, and it operates by linearizing the system dynamics and measurement models around the current estimated state. This linearization allows the EKF to account for the uncertainties in process and measurement noise, thus providing accurate tracking of the system’s state over time.

Key features of the EKF include its ability to provide more accurate estimates by modeling the system’s dynamics and its inherent uncertainties. It is widely used in fields such as robotics, navigation, and aerospace, where nonlinearity is common. Through continuously updated state estimates, the EKF effectively improves the accuracy and reliability of the estimated state, making it a valuable tool for solving various control and estimation problems.

The following figure illustrates the operation of the EKF:

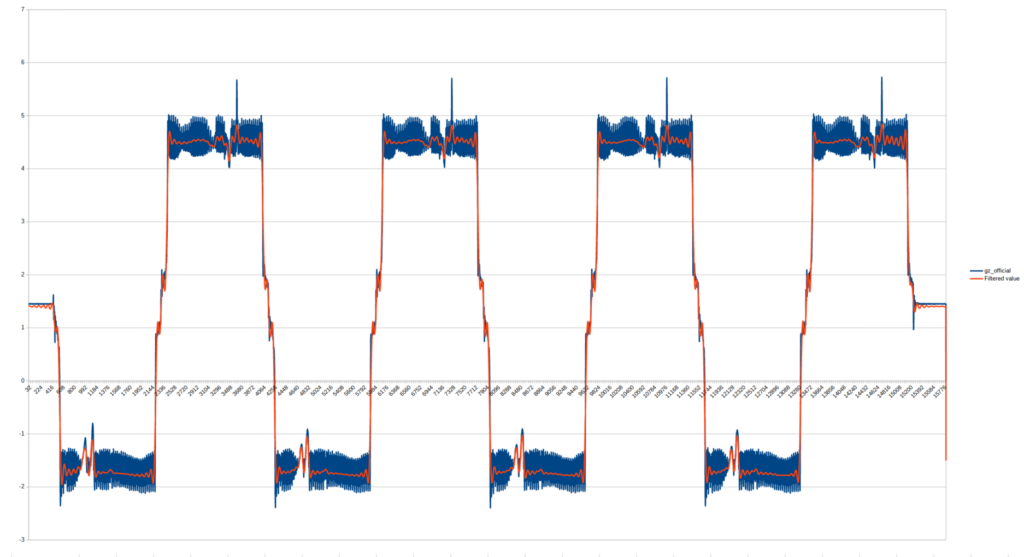
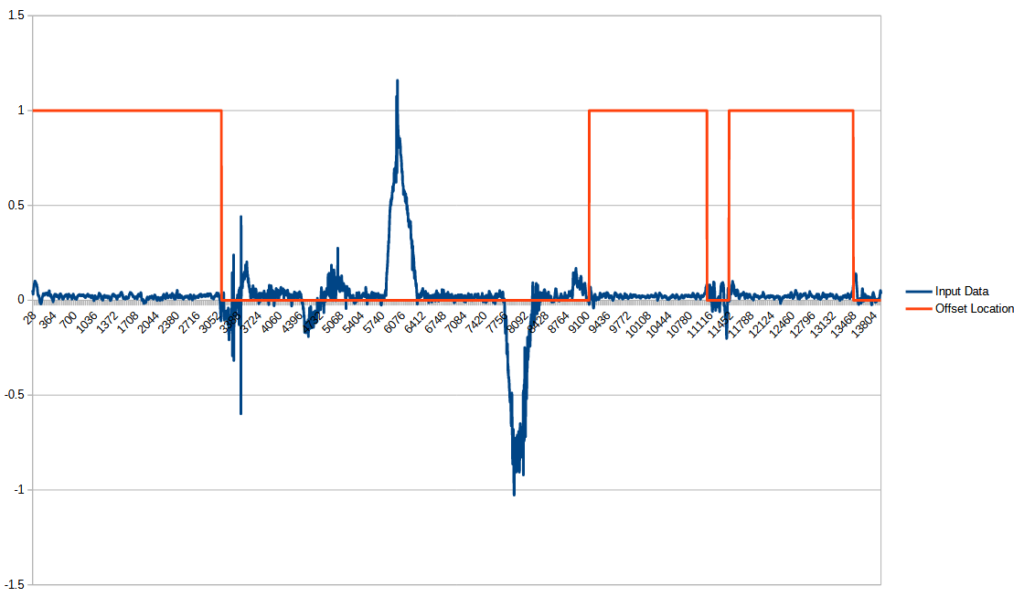
The baseline noise arising from the operation of the gyroscope is referred to as drift in the literature. This error is caused by the system’s continuous vibrations and manufacturing inaccuracies, and it depends on the sensor’s orientation and temperature. It is challenging to manage because the system can yield completely random results due to unforeseen events. I found the best solution to be recalculating this drift value every time the sensor comes to a rest position. I designated this as adaptive offset. In the following image, I illustrate the determination of these resting positions during measurement:

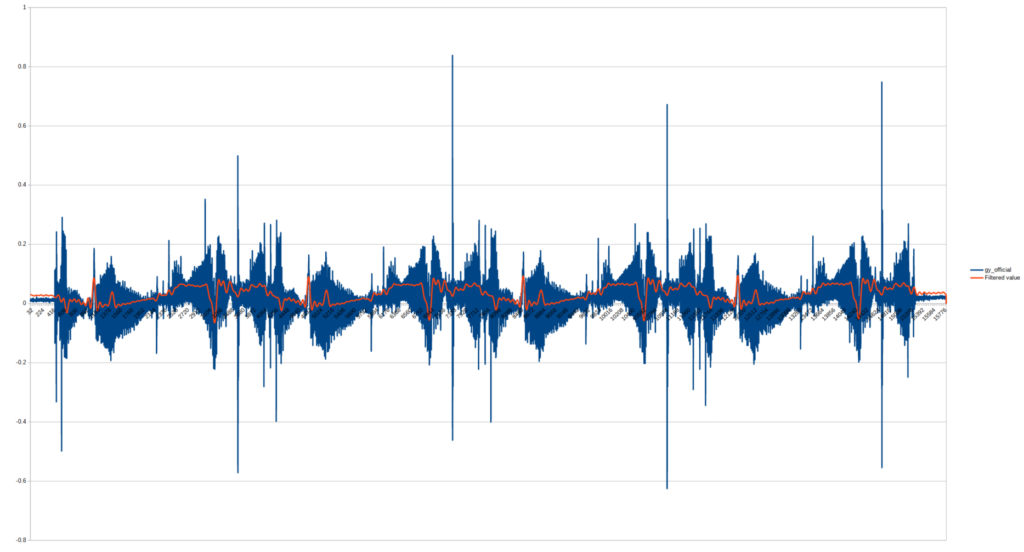
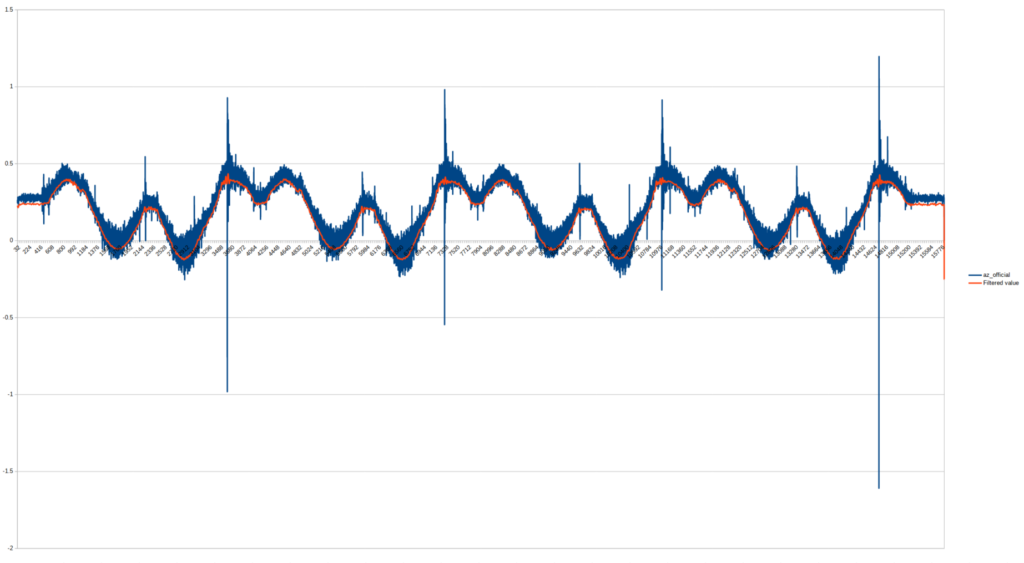
As a result of the aforementioned processing, we obtain a stable result with reduced noise. The following two images show a series of measurements, where the phenomenon of drift is clearly observable, as well as the filtering of smaller noises from the top measurement:

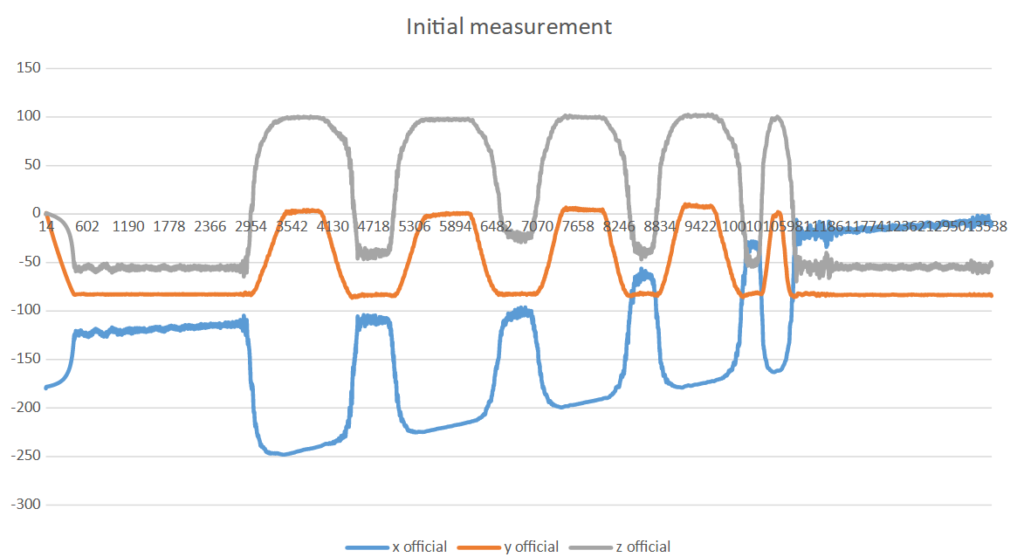
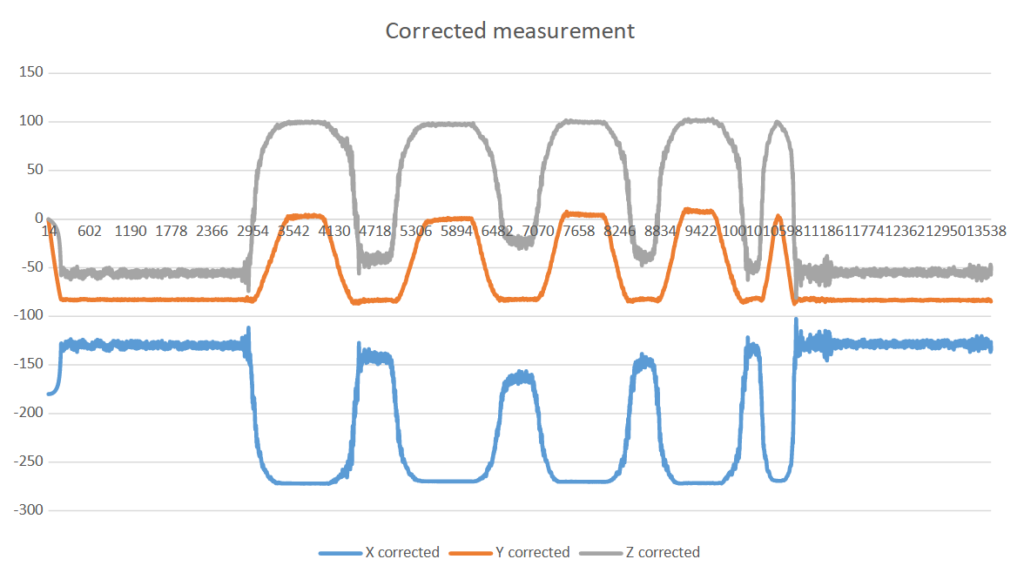
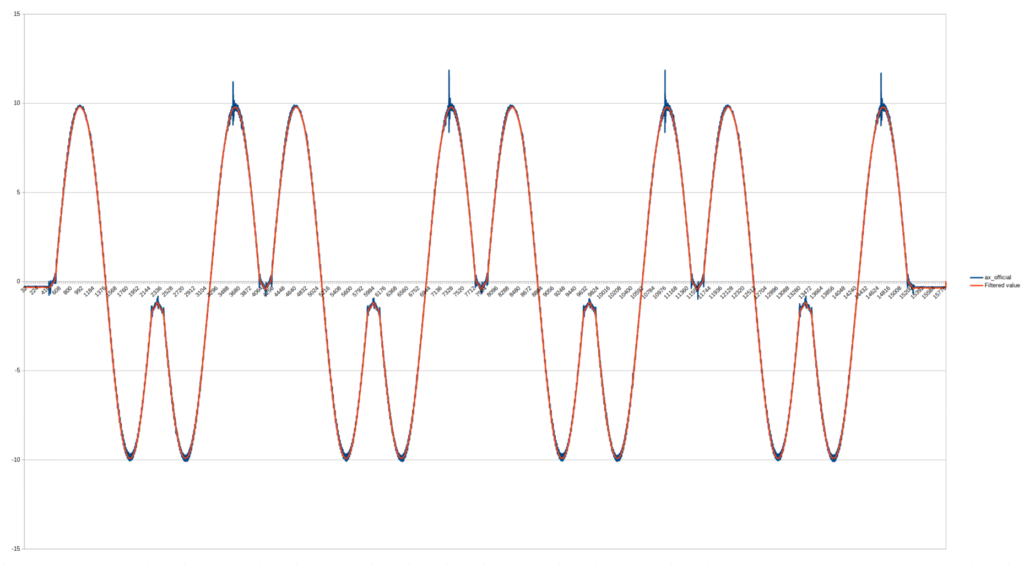
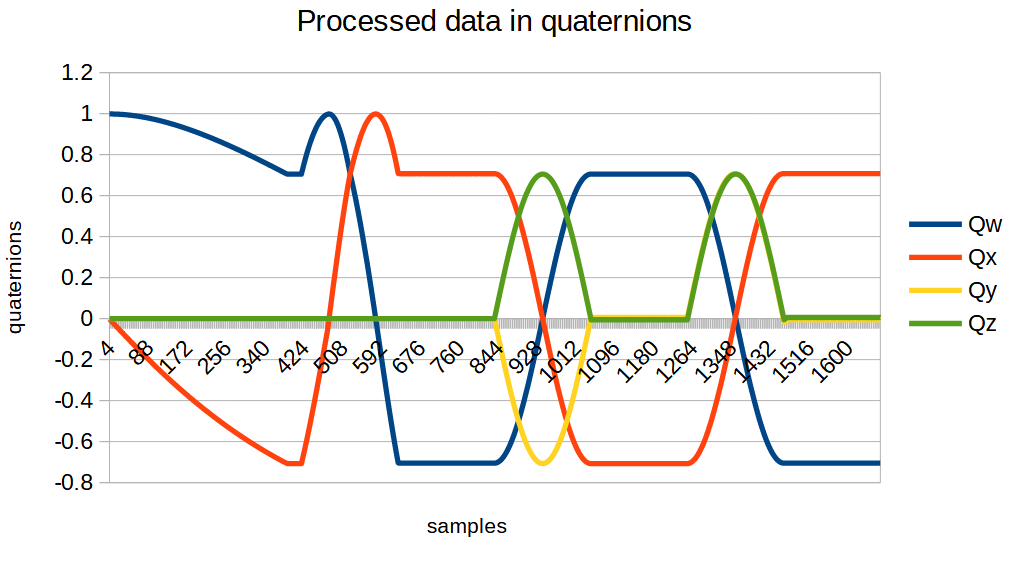
Finally, I would like to illustrate the results of the algorithms applied above, as well as the Madqwick Quaternion Update Filter, in the following four images:

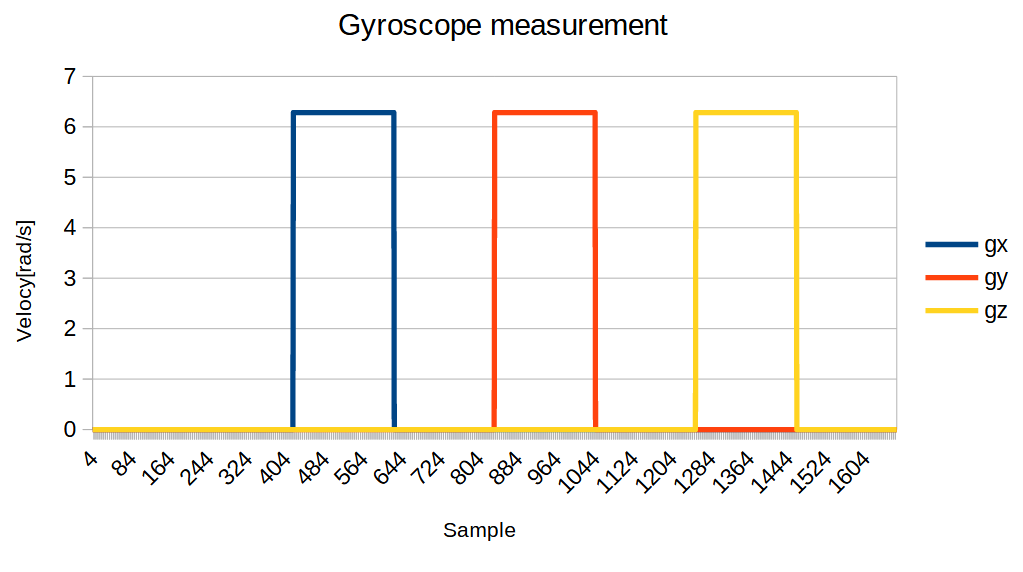
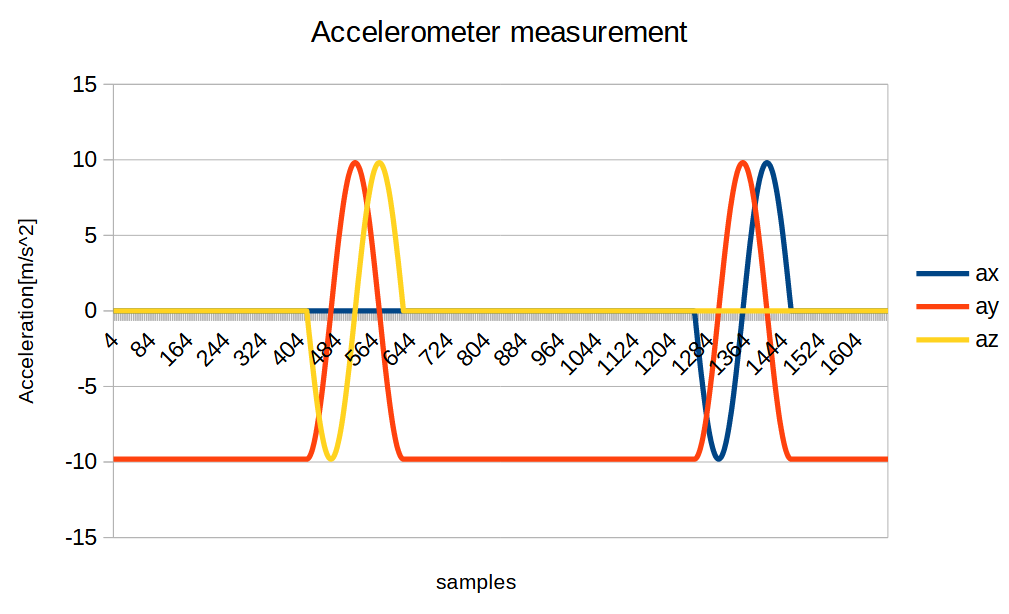
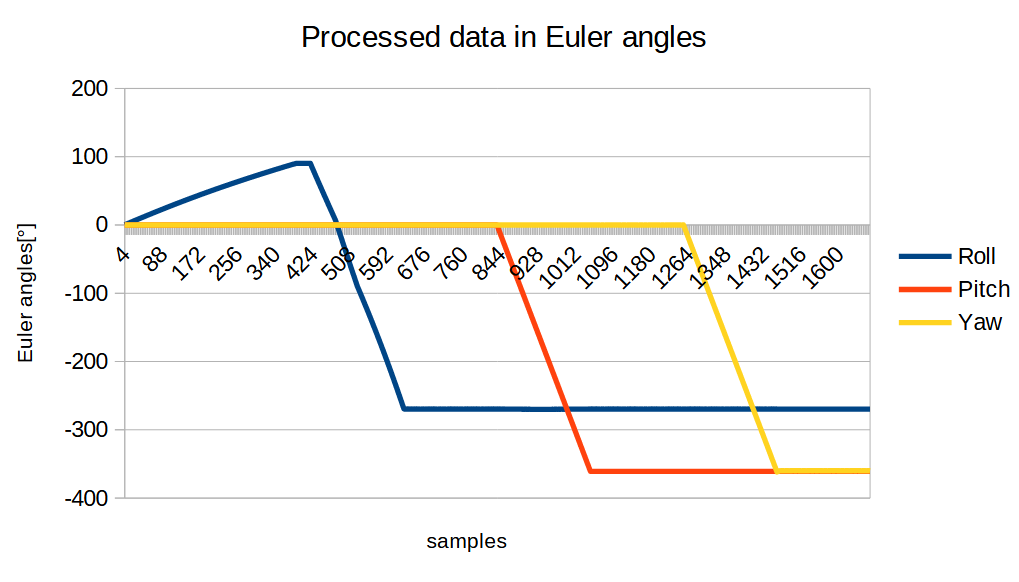
Conclusion

This appeared to be a complex and diverse programming task that required a broad perspective. My experience as a mechatronics engineer greatly facilitated my work, as it made it much easier for me to understand the physical parameters and the operation of the sensors and apply appropriate algorithms to them.